决策树

决策树生成的原理及算法研究

概述

决策树是一个预测模型；代表的是对象属性与对象值之间的一种映射关系。

决策树的思想：从数据集合中的知识信息提取出一系列规则，并根据规则逐步构建树

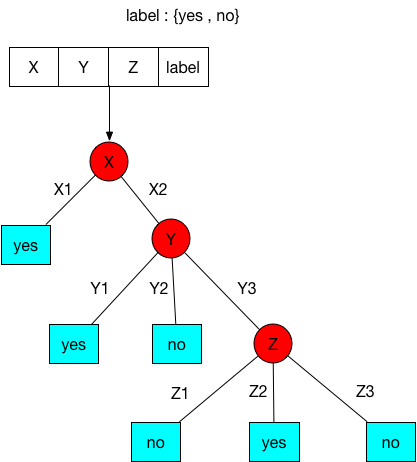
如上图，一般的决策树包含三种类型的节点（类似流程图）：

1. Decision nodes：用矩形表示，如1,2；
2. Chance nodes：用圆形表示
3. End nodes：用三角形表示

优缺点：

1. 优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据
2. 缺点：可能会产生过度匹配问题；对于各类别样本数量不一致的数据，信息增益的结果会更偏向于更多数值的特征

适用数据类型：数值型和标称型

特征选择

熵(entropy)被定义为信息的期望值，表示随机变量不确定性的度量。

如果待分类的事情可能被划分在多个分类中，则符号$x_i$的信息定义为：

$$l(x_i) = - \log_{2}p(x_i)$$

其中$p(x_i)$是选择该分类的概率。

熵的公式定义如下：

$$H = - \sum_{i=1}^n p(x_i) \log_2 p(x_i)$$

其中n是分类的数据。意思是一个变量可能的变化越多，它携带的信息量越大

设有随机变量(X,Y)，其联合概率分布为

$$P(X = x_i , Y = y_i) = p_{ij} \qquad i=1,2,\cdots,n;\quad j=1,2,\cdots,m$$

条件熵H(Y|X)表示在已经随机变量X的条件下随机变量Y的不确定性，定义为

$$H(Y|X) = \sum_{i=1}^n p_i H(Y | X = x_i)$$

# 如果数据集dataset = [[x1 , x2 , ... , xn , label] , ... ] 则香农熵计算公式如下
def calcShannonEnt(dataset) :
	labelCount = len(dataset)
    labelCounts = {}
    # 得到各标签出现的次数
    for row in dataset :
        label = row[-1]
        if label not in labelCounts.keys() :
			labelCounts[label] = 0
        labelCounts[label] += 1
    shannonEnt = 0.0
    for label in labelCounts :
        # 标签出现的概率
        p = float(labelCounts(label)) / labelCount
        shannonEnt -= prob * log(p , 2)
	return shannonEnt

信息增益

信息增益表示得知特征X的信息而使得Label{Y}的信息不确定性减少的程度。特征A对训练数据集D的信息增益g(D,A)，定义为数据集D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即

$$g(D,A) = H(D) - H(D | A)$$

一般地，熵H(Y)与条件熵H(Y|X)之差称为互信息.决策树学习中的信息增益等价于训练数据集中类与特征的互信息

信息增益比

以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题.使用信息增益比(information gain ratio)可以对这一问题进行校正.

定义：特征A对训练数据集D的信息增益比$g_R(D,A)$定义为其信息增益g(D,A)与训练数据集D关于特征A的值的熵$H_A(D)$之比，即

$$g_R(D,A) = {g(D,A) \over H_A(D)}$$

其中，$H_A(D) = - \sum_{i=1}^n {|D_i| \over |D|} \log_{2} {|D_i| \over |D|} $ ，n是特征A取值的个数

决策树生成

决策树的构建步骤：

1. 收集并准备数据：数值型数据必须离散化
2. 特征选择：计算数据集中各特征的信息增益值，选取最优特征(信息增益值最大)划分数据集
3. 类别划分：计算最优特征中对应的最优类别
4. 创建子树：递归执行2，直到无特征划分数据集

ID3算法

核心：在决策树各个结点上应用信息增益准则选择特征，递归地构建决策树

输入：数据集D，特征集A，阈值$\varepsilon$

输出：决策树T

1. 若D中所有实例都属于同一label，则T为单结点树，并将该label作为其取值，返回T
2. 若$A=\varnothing$，则T为单结点树，并将D中label出现次数最多的作为其取值，返回T
3. 否则，计算A特征集中对D的信息增益，选取最大的值作为最优特征$A_g$
4. 若$A_g$的信息增益小于$\varepsilon$ ，则T为单结点树，并将D中label出现次数最多的作为其取值，返回T
5. 否则对$A_g$中的每一个取值$a_i$，依$A_g = a_i$将D划分为若干个非空子集$D_i , i = 1,2,\cdots,k$，其中k为$A_3$的取值个数；将$D_i$中label出现次数最多的作为其取值，构建子结点，由结点及其子结点构建树T并返回
6. 对第$i$个子结点，以$D_i$为训练集，以不包括$A_g$的新$A_k$作为特征集，递归地调用上述步骤，得到子树$T_i$并返回

C4.5的生成算法

与ID3算法相似，只需将ID3算法中选择特征用的信息增益值替换为信息增益比

Example

给定以下数据集，为其构建决策树

（1）计算熵和信息增益

label个数： 是（9） 否（6）

$$H(D) = - {9 \over 15} \log_2 {9 \over 15} - {6 \over 15} \log_2 {6 \over 15} = 0.971$$

分别以$A_1$，$A_2$，$A_3$ ，$A_4$表示年龄、有工作、有房子和信贷情况4个特征，则各自信息增益如下

以年龄为例，count(青年) = 5 , 其中类别是（2），否（3）

count(中年) = 5 , 其中类别是（3），否（2）

count(老年) = 5 , 其中类别是（4），否（1）

$$\begin{equation} \begin{split} g(D,A_1) &= H(D) - \left[ {5 \over 15}H(D_1) + {5 \over 15}H(D_2) + {5 \over 15}H(D_2) \right] \\ &= 0.971 - \left[ {5 \over 15}(-{2 \over 5}\log_2{2 \over 5}-{3 \over 5}\log_2{3 \over 5}) + \\ {5 \over 15}(-{3 \over 5}\log_2{3 \over 5}-{2 \over 5}\log_2{2 \over 5}) + {5 \over 15}(-{4 \over 5}\log_2{4 \over 5}-{1 \over 5}\log_2{1 \over 5}) \right] \\ &= 0.971 - 0.888 \\ &= 0.083 \end{split} \end{equation}$$

同理可计算出

$$\begin{aligned} & g(D , A_2) = 0.324 \\ & g(D , A_3) = 0.420 \\ & g(D , A_4) = 0.363 \\ \end{aligned}$$

最后比较信息增益值，由于$A_3$的信息增益值最大，则选取$A_3$作为最优特征

（2）划分数据集

根据$A_3$的取值将数据集D划分为若干个非空$D_i , i = 1,2,\cdots,k$，其中k为$A_3$的取值个数；若$D_i$中所有实例label相同，则将此结点置为叶结点，这里的当有自己的房子=是，label全等于是，所以当特征$A_3$=是，label=是；否则对划分的数据集$D_i$递归执行(1),(2)步骤。

决策树的剪枝

使用决策树生成算法产生的决策树，对训练数据的分类很准确，但对于未知的特征取值的分类却没有那么准确，即出现过拟合现象，过拟合的原因在于学习时过多地考虑如何提高对训练数据的正确分类，从而构建出过于复杂的决策树。为了解决这个问题，我们需要考虑降低决策树的复杂度，对已生成的决策树进行简化 — 称为剪枝

剪枝：从已生成的决策树上裁掉一些子树或叶结点，并将其根结点或父结点作为新的叶结点，从而简化树模型

决策树的剪枝往往通过极小化决策树整体的损失函数来实现。设树T的叶结点（可以理解为特征的每个取值）个数为|T|，t是树T的叶结点，该叶结点有$N_t$个样本点，其中k类的样本点有$N_{tk}$个，$k=1,2,\cdots,K$，$H_t(T)$为叶结点t上的熵，$\alpha \ge 0$为参数，则决策树学习的损失函数可以定义为

$$C_\alpha(T) = \sum_{t=1}^{|T|}N_t H_t(T) + \alpha |T|$$

其中叶结点t的熵为

$$H_t(T) = - \sum_{k=1}^K {N_{tk} \over N_t} \log_2{N_{tk} \over N_t}$$

令

$$C(T) = \sum_{t=1}^{|T|}N_t H_t(T) = - \sum_{t=1}^{|T|} \sum_{k=1}^K N_{tk} \log_2{N_{tk} \over N_t}$$

则

$$C_\alpha(T) = C(T) +\alpha |T|$$

C(T)表示模型对训练数据的预测误差，即模型与训练数据的拟合程度，|T|表示模型复杂度，参数$\alpha \ge 0$控制两者之间的影响.较大的$\alpha$促使其得到简单的树，较小的$\alpha$促使其得到较复杂的树，$\alpha = 0$意味着只考虑模型与训练数据的拟合程度，不考虑模型的复杂度

树的剪枝算法

输入：生成算法产生的决策树T，参数为$\alpha$

输出：修剪后的子树$T_\alpha$

（1）计算每个结点的熵

（2）递归地从树的叶结点向上回缩

设一组叶结点回缩到其父节点之前与之后的整体树分别为$T_B$与$T_A$，其对应的损失函数值分别是$C_\alpha (T_B)$与$C_\alpha (T_A)$，如果$C_\alpha (T_A) \le C_\alpha (T_B)$，则进行剪枝，将其父节点变为新的叶结点

FYI

DecisionTree

信息增益

机器学习实战

统计学习方法