二叉查找树的Java实现

最近在闲看博客时看到一篇专门写红黑树的实现原理，以Java的TreeMap为例讲解，写的很不错，仔细看下来发现很多地方不是很理解，毕竟没有对树的理解并没有很深，所以决定一步一步的将与树相关的扩展实现都了解一遍，沿着下面的学习路线开始，大家也可以参考以下。

• 树的基本知识
• 二叉树的知识
• 二叉查找树
• 平衡二叉树
• 红黑树
• B树，B-树，B+树

附上上面的将红黑树的blog：史上最清晰的红黑树讲解

树的基本概念

树Tree是n（n≥0）个结点的有限集。在任意一棵非空树中：（1）有且仅有一个特定的被称为根root的结点；（2）当n>1时，其余结点可分为m（m>0）个互不相交的有限集T1，T2，…，Tm，其中每一个集合本身又是一棵树，并且称为根的子树SubTree。

1. 结点拥有的子树数称为结点的度（Degree）。度为0的结点称为叶子（Leaf）或终端结点。度不为0的结点称为非终端结点或分支结点。
2. 树的度是树内各结点的度的最大值。
3. 结点的子树的根称为该结点的孩子（Child），相应地，该结点称为孩子的双亲（Parent）。
4. 结点的层次（Level）是从根结点开始计算起，根为第一层，根的孩子为第二层，依次类推。树中结点的最大层次称为树的深度（Depth）或高度。
5. 如果将树中结点的各子树看成从左至右是有次序的（即不能互换），则称该树为有序树，否则称为无序树。

二叉树的基本概念

二叉树（Binary Tree）的特点是每个结点至多具有两棵子树（即在二叉树中不存在度大于2的结点），并且子树之间有左右之分。

二叉树的性质：

1. 在二叉树的第i层上至多有2i-1个结点（i≥1）。
2. 深度为k的二叉树至多有2k-1个结点（k≥1）。
3. 对任何一棵二叉树，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1。
4. 具有n个结点的完全二叉树的深度为不大于log2n的最大整数加1。

5. 如果对一棵有n个结点的完全二叉树的结点按层序编号（从第1层到最后一层，每层从左到右），则对任一结点i（1≤i≤n）,有

   a、如果i=1,则结点i是二叉树的根，无双亲；如果i>1，则其双亲是结点x（其中x是不大于i/2的最大整数）。

   b、如果2i>n，则结点i无左孩子（结点i为叶子结点）；否则其左孩子是结点2i。

   c、如果2i+1>n，则结点i无右孩子；否则其右孩子是结点2i+1。

二叉查找树

二叉查找树（BinarySearch Tree，也叫二叉搜索树，或称二叉排序树Binary Sort Tree）或者是一棵空树，或者是具有下列性质的二叉树：

1. 若它的左子树不为空，则左子树上所有结点的值均小于它的根结点的值；
2. 若它的右子树不为空，则右子树上所有结点的值均大于它的根结点的值；
3. 它的左、右子树也分别为二叉查找树。

结点定义：

public class TreeNode<T> {

	/**
	 * 结点的值
	 */
	private T value;

	/**
	 * 左结点
	 */
	private TreeNode<T> left;
	
	/**
	 * 右结点
	 */
	private TreeNode<T> right;
	
	/**
	 * 父亲结点
	 */
	private TreeNode<T> parent;

	/**
	 * 频率
	 */
	private int freq;

}

插入

根据二叉查找树的性质，插入一个节点的时候，如果根节点为空，就此节点作为根节点，如果根节点不为空，就要先和根节点比较，如果比根节点的值小，就插入到根节点的左子树中，如果比根节点的值大就插入到根节点的右子树中，如此递归下去，找到插入的位置。重复节点的插入用值域中的freq标记。如图2是一个插入的过程。

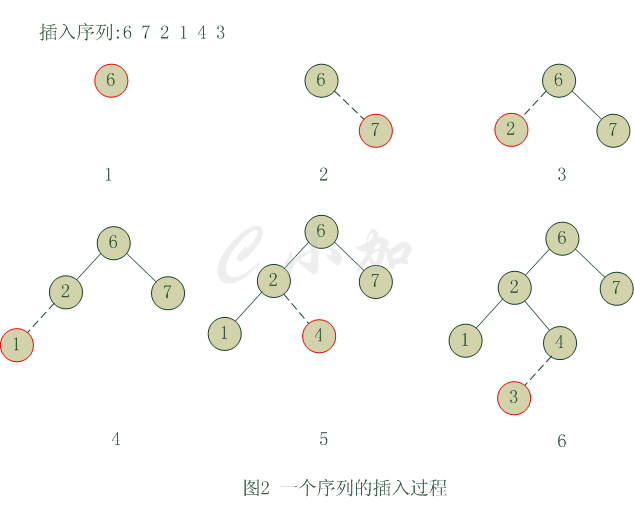
二叉查找树的时间复杂度要看这棵树的形态，如果比较接近一一棵完全二叉树，那么时间复杂度在O(logn)左右，如果遇到如图3这样的二叉树的话，那么时间复杂度就会恢复到线性的O(n)了。

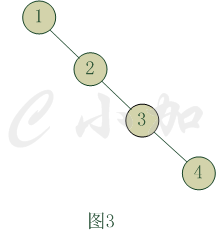
平衡二叉树会很好的解决如图3这种情况。

核心代码如下：

private boolean insert(SearchNode<T> curr, SearchNode<T> insertNode, SearchNode<T> parent, boolean currIsLeft) {
	if (curr == null) {
		curr = insertNode;
		if (currIsLeft) {
			parent.setLeft(curr);
		} else {
			parent.setRight(curr);
		}
	} else {
		int result = curr.getValue().compareTo(insertNode.getValue());
		// 如果当前值大于插入的值
		if (result > 0) {
			return insert((SearchNode<T>)curr.getLeft(), insertNode, curr, true);
		} else if (result < 0) {
			return insert((SearchNode<T>)curr.getRight(), insertNode, curr, false);
		}else {
			curr.freq++;
		}
	}
	return true;
}

查找

在二叉查找树中查找x的过程如下：

1. 若二叉树是空树，则查找失败。
2. 若x等于根结点的数据，则查找成功，否则。
3. 若x小于根结点的数据，则递归查找其左子树，否则。
4. 递归查找其右子树。

核心代码如下：

protected TreeNode<T> find0(TreeNode<T> node, T value) {
	if (node == null) {
		return null;
	}
	int result = node.getValue().compareTo(value);
	if (result > 0) {
		return find0(node.getLeft(), value);
	} else if (result < 0) {
		return find0(node.getRight(), value);
	}
	return node;
}

删除

删除会麻烦一点，如果是叶子节点的话，直接删除就可以了。如果只有一个孩子的话，就让它的父亲指向它的儿子，然后删除这个节点。图4显示了一棵初始树和4节点被删除后的结果。先用一个临时指针指向4节点，再让4节点的地址指向它的孩子，这个时候2节点的右儿子就变成了3节点，最后删除临时节点指向的空间，也就是4节点。

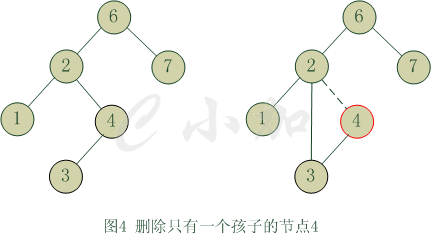
删除有两个儿子的节点会比较复杂一些。一般的删除策略是用其右子树最小的数据代替该节点的数据并递归的删除掉右子树中最小数据的节点。因为右子树中数据最小的节点肯定没有左儿子，所以删除的时候容易一些。图5显示了一棵初始树和2节点被删除后的结果。首先在2节点的右子树中找到最小的节点3，然后把3的数据赋值给2节点，这个时候2节点的数据变为3，然后的工作就是删除右子树中的3节点了，采用递归删除。

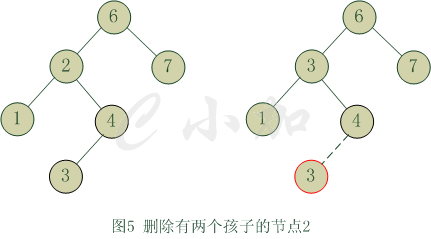
我们发现对2节点右子树的查找进行了两遍，第一遍找到最小节点并赋值，第二遍删除这个最小的节点，这样的效率并不是很高。你能不能写出只查找一次就可以实现赋值和删除两个功能的函数呢？

如果删除的次数不是很多的话，有一种删除的方法会比较快一点，名字叫懒惰删除法：当一个元素要被删除时，它仍留在树中，只是多了一个删除的标记。这种方法的优点是删除那一步的时间开销就可以避免了，如果重新插入删除的节点的话，插入时也避免了分配空间的时间开销。缺点是树的深度会增加，查找的时间复杂度会增加，插入的时间可能会增加。

核心代码如下：

protected void deleteNode(TreeNode<T> deleteNodeParent, TreeNode<T> deleteNode) {
	if (deleteNodeParent == null) {
		// 左右子树都为空
		if (deleteNode.getLeft() == null && deleteNode.getRight() == null) {
			root = null;
		} else if (deleteNode.getLeft() == null || deleteNode.getRight() == null) {
			// 存在左子树或右子树
			if (deleteNode.getLeft() != null) {
				root = deleteNode.getLeft();
			} else {
				root = deleteNode.getRight();
			}
		} else {
			// 左右子树都不为空
			TreeNode<T> temp = deleteNode;
			TreeNode<T> rightLeft = deleteNode.getRight();
			while (rightLeft.getLeft() != null) {
				temp = rightLeft;
				rightLeft = rightLeft.getLeft();
			}
			if(temp == deleteNode) {
				deleteNode.setRight(rightLeft.getRight());
			}else {
				temp.setLeft(rightLeft.getRight());
			}
			deleteNode.setValue(rightLeft.getValue());	
		}
	} else {
		// 左右子树都为空
		if (deleteNode.getLeft() == null && deleteNode.getRight() == null) {
			// 根结点
			if (deleteNodeParent.getLeft() == deleteNode) {
				deleteNodeParent.setLeft(null);
			} else {
				deleteNodeParent.setRight(null);
			}
		} else if (deleteNode.getLeft() == null || deleteNode.getRight() == null) {
			// 存在左子树或右子树
			if (deleteNode.getLeft() != null) {
				if (deleteNodeParent.getLeft() == deleteNode) {
					// 如果待删除结点是左结点，且其存在左结点
					deleteNodeParent.setLeft(deleteNode.getLeft());
				} else {
					// 如果待删除结点是左结点，且其存在右结点
					deleteNodeParent.setRight(deleteNode.getLeft());
				}
			} else {
				if (deleteNodeParent.getRight() == deleteNode) {
					deleteNodeParent.setRight(deleteNode.getRight());
				} else {
					deleteNodeParent.setLeft(deleteNode.getRight());
				}
			}
		} else {
			// 左右子树都不为空
			TreeNode<T> temp = deleteNode;
			TreeNode<T> rightLeft = deleteNode.getRight();
			while (rightLeft.getLeft() != null) {
				temp = rightLeft;
				rightLeft = rightLeft.getLeft();
			}
			if(temp == deleteNode) {
				deleteNode.setRight(rightLeft.getRight());
			}else {
				temp.setLeft(rightLeft.getRight());
			}
			deleteNode.setValue(rightLeft.getValue());	
		}
	}

}

具体实现代码请查看：https://github.com/mastery001/study/blob/master/study-datastruct/src/main/java/tree/search/BinarySearchTree.java

参考资料：

• 二叉查找树—查找、删除、插入（Java实现）
• 一步一步写二叉查找树